IEEE 754
Systems in Rust
Announcements
- Welcome to Systems in Rust
- Action Items:
- “SHA-512” is due on next Friday
- Lecture on numbers, inspired by the lab, while we wait.
Today
- Understand precision through the lens of floats.
- Understand the basics of floats
- Understand the language of floats
- Get a feel for when further investigation is required
Citation
- Yoinked
- url
- Author John Farrier, Booz Allen Hamilton
Mission Statement
- I’m a normal person.
- I think
5/2is2.5or perhaps 2½.
- I think
- I’m a scientist.
- I’m solving “Black-Scholes”
- Does anyone know what this is doing? \[ d_2 = d_1 - \sigma\sqrt{T - t} = \frac{1}{\sigma\sqrt{T - t}}\left[\ln\left(\frac{S_t}{K}\right) + \left(r - q - \frac{1}{2}\sigma^2\right)(T - t)\right] \]
Common Fallacies
- “Floating point numbers are numbers”
max(count())Pinocchios
- “It’s floating point error”
- “All floating point involves magical rounding errors”
- “Linux and Windows handle floats differently”
- “Floating point represents an interval value near the actual value”
Common Fallacies 2.0
Anatomy of IEEE Floats
IEEE Float Specification
- IEEE 754-1985, IEEE 854-1987, IEEE 754-2008
- These are paywalled.
- Those are years.
- Provide for portable, provably consistent math
- Consistent, not correct.
Assurances
- Ensure some significant mathematical identities hold true:
- \(x + y = y + x\)
- Symmetry of addition
- \(x + 0 = x\)
- Additive identity
- \(x = y \implies x - y = 0\)
- Identity under subtraction
- \(x + y = y + x\)
Assurances 2.0
\[ \frac{x}{\sqrt{x^2+y^2}} \leq 1 \]
- What is missing?
IEEE Float Specification
- Ensure every floating point number is unique
- Ensure every floating point number has an opposite
- Zero is a special case because of this
- Specifies algorithms for addition, subtraction, multiplication, division, and square-root
- Not really operations/relations! They are algorithms.
Aside: Scientific Notation
- In scientific notation, nonzero numbers are written in the form
\[a \times 10^b\]
Aside: Explanation
- In scientific notation, nonzero numbers are written in the form
\[a \times 10^b\]
- \(a\) (the coefficient or mantissa) is a number greater than or equal to 1 and less than 10 (\(1 \le |a| < 10\)).
- \(10\) is the base.
- \(b\) (the exponent) is an integer.
Aside: Physical Examples
Speed of light: The speed of light in a vacuum is approximately \(300,000,000 \text{ m/s}\) \[ 3 \times 10^8 \text{ m/s} \]
Mass of an electron: The mass of an electron is approximately \(0.00000000000000000000000000091093837 \text{ g}\). \[ 9.1093837 \times 10^{-28} \text{ g} \]
Aside: Economic Examples
- We can use social science numbers.
- Labor Market Outcomes of College Graduates by Major
- Computer Science majors in 2023 have a $80,000 median wage “early career”
- \(8.0000 \times 10^4\)
- And 6.1% unemployment
- \(6.1 \times 10^{-2}\)
IEEE Layout
- An approximation using scientific notation
- \(x = -1^s \times 2^e \times 1.m\)
- \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1.\text{mantissa}\)
- Where the mantissa is the technical term for the the digits after the decimal point.
With Binary
- \(x = -0b1^{\text{0b0}} \times 0b10^{\text{0b10000000}} \times 0b1.10010010000111111011011\)
- Express in memory as the concatenation:
0b0to0b10000000to0b1001001000011111101101101000000010010010000111111011011
Singles and Doubles
- 32 - bits = 1 sign bit + 8 exponent bits + 23 mantissa bits
0b0to0b10000000to0b10010010000111111011011
- 64 - bits = 1 sign bit + 12 exponent bits + 52 mantissa bits
Understanding check
- What is the probability a real number \(a \in \mathbb{R}\) has an exact float representation?
- What is the probability an integer \(n \in \mathbb{Z}\) has an exact float representation?
- What is the probability a course number \(n < 600\) has an exact float representation?
Special Floats - NaN
- Divide by Zero
- 1 / 0
- Not a Number (NaN)
Special Floats - inf
- Signed Infinity
- Overflow protection
Infinity is signed
- We can get negative infinity through a variety of means.
- We note that this suppresses the overflow error use
() - In some languages this is not ever regarded as an overflow error, like Julia (where we have to use larger powers due to the f64 default)
Signed Zero
- Signed Zero
- Underflow protection, preserves sign
- 0 =− 0
- Works in base Python (e.g. don’t need NumPy).
- Couldn’t get it to work in Julia actually (went to -inf or NaN)
Simple Example
- Floating point is great because it will work exactly how you expect.
- More or less.
Simple Example
- We shouldn’t be suprised by this!
>>> _ = [print(f"{f32(i/10):1.100}") for i in range(1,4)]
0.100000001490116119384765625
0.20000000298023223876953125
0.300000011920928955078125
>>> _ = [print(f"{f64(i/10):1.100}") for i in range(1,4)]
0.1000000000000000055511151231257827021181583404541015625
0.200000000000000011102230246251565404236316680908203125
0.299999999999999988897769753748434595763683319091796875Storage of 1.
- \(x = -1^s \times 2^e \times 1.m\)
- \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1.\text{mantissa}\)
- \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1 + \text{mantissa} \times \frac{1}{2^n}\)
- \(1 = -1^0 \times 2^0 \times (1 + 0 \times \frac{1}{2^n}\)
- So each of the sign bit, the base, and the mantissa are zero.
- I should note I was unable to reproduce this in Rust or C.
- I’m not really a floating pointer.
Except…
- This is actually a little bit fake.
$ cat src/main.rs
fn main() {
let x:f32 = 1.0;
println!("{:032b}", x.to_bits());
}
$ cargo run
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.00s
Running `target/debug/bits`
00111111100000000000000000000000- What is that?
Shift 127
- The IEEE 754 binary format specifies a hardware implementation of such that the exponent, be it positive or negative, in binary formats is stored as an unsigned number that has a fixed “bias” added to it.
- In the case of 32 bit floats, the bias is 127.
Breakdown
- Take the following:
- That is:
- Sign bit of
0 - Exponent of
01111111- All zeroes and all ones are reserved for
NaN,inf, etc.
- All zeroes and all ones are reserved for
- Mantissa of 23 zeroes.
- Sign bit of
How precise?
- I have referred to
f32as having “32 bits of precision”. - How much precision is that?
- Well, let’s set the least significant bit of the mantissa to one.
“Epsilon”
- What do we get?
$ cargo run
Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.00s
Running `target/debug/bits`
00111111100000000000000000000001
1.00000011920928955078125000000000- We refer to this value (less one) as machine epsilon, or perhaps \(\varepsilon\).
- The difference between 1.0 and the next available floating point number.
- Much lower, of course, with double and quad precision.
Easier: “Sig figs”
| Format | Sign | Exp. | Mant. | Bits | Bias | Prec. | Significance |
|---|---|---|---|---|---|---|---|
| Half | 1 | 5 | 10 | 16 | 15 | 11 | 3-4 |
| Single | 1 | 8 | 23 | 32 | 127 | 24 | 6-9 |
| Double | 1 | 11 | 52 | 64 | 1023 | 53 | 15-17 |
| Quad | 1 | 15 | 112 | 128 | 16383 | 113 | 33-36 |
Sig figs
- IEEE 754 was intended for scientific computing
- That is, not systems computing, software etc.
- Useful to us to think about information and how bits work.
Small Values
- For 32-bit floats, the minimum base 10 exponent is -36.
- How is \(1.0 \times 10^{-37}\) represented?
Test it
- Write a simple test…
src/main.rs
- Results are as expected.
“Denormalized Number”
- Numbers that have a zero exponent
- Required when the exponent is below the minimum exponent
- Helps prevent underflow
- Generally speaking, if you are using one these, the math is about to get wronger than you’d think.
- The good (???) language C++ provides a
std::nextafterfor which Rust crates exist.
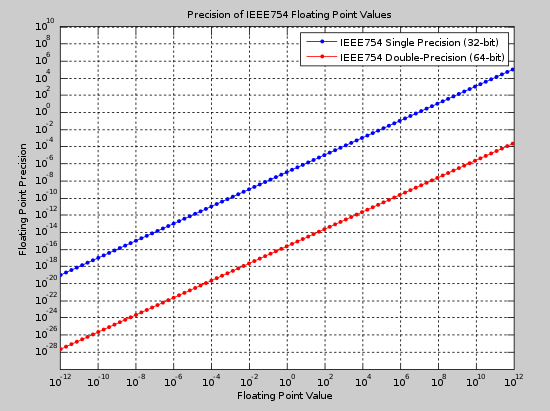
Floating Point Precision
- Representation is not uniform between numbers
- Most precision lies between 0.0 and 0.1
- Precision falls away
Visually
Floating Point Precision
The number of floats from 0.0
- … to 0.1 = 1,036,831,949
- … to 0.2 = 8,388,608
- … to 0.4 = 8,388,608
- … to 0.8 = 8,388,608
- … to 1.6 = 8,388,608
- … to 3.2 = 8,388,608
Errors in Floating Point
- Storage of \(\pi\)
>>> from numpy import pi as pi
>>> # copy paste Wolfram|Alpha
>>> '3.14159265358979323846264338327950288419716939937510582097494459230781640628'
'3.14159265358979323846264338327950288419716939937510582097494459230781640628'
>>> f'{pi:1.100}'
'3.141592653589793115997963468544185161590576171875'- They differ fairly early on!
Measuring Error: “Ulps”
- Units in Last Place
Haskell
- Usually ULP is taught using Haskell.
- I’ll translate to .py/.rs
Generators
- By convention we check number theoretic results with lazily evaluated generator expressions in Python.
- The following generators all powers of two for a which adding one does not change the value within Python floating points.
Iterators
- Rust doesn’t require iterators, supporting the infinite iterator by default using
unwrap.
let x = (0..).find(|&i| f64::powi(2.0, i) + 1.0 == f64::powi(2.0, i)).unwrap();
let base = f64::powi(2.0, x);
// Prints the result (2^53 = 9007199254740992.0)
println!("2.0 ** x + 0.0 = {:.1}", base);
println!("2.0 ** x + 1.0 = {:.1}", base + 1.0);- I haven’t used
findbefore, this is an LLM donation to our knowledge base. - By the way, that is basically
2 ** 53and there are 52 bits of mantissa precision.
On “Ulps”
- We can measure error using ULPs.
The gap between the two floating-point numbers nearest to x, even if x is one of )them.
Rounding
- We have some guarantees:
- IEEE 754 requires that that elementary arithmetic operations are correctly rounded to within 0.5 ulps
- Transcendental functions are generally rounded to between 0.5 and 1.0 ulps
- Transcendental as in \(\pi\) or \(e\)
- ~9 ulps
Relative Error
- The difference between the “real” number and the approximated number, divided by the “real” number.
- So for
piinf32, around \(2.9 \times 10^{-8}\)
Rounding Error
- Induced by approximating an infinite range of numbers into a finite number of bits
- Rounding is:
- Towards the nearest
- Towards zero
- Towards positive infinity (round up)
- Towards negative infinity (round down)
Rounding Error
- What about rounding the half-way case? (i.e. 0.5)
- Round Up vs. Round Even
- Correct Rounding:
- Basic operations (add, subtract, multiply, divide, sqrt) should return the number nearest the mathematical result.
- If there is a tie, round to the number with an even mantissa
Implementation
- “Guard Bit”, “Round Bit”, “Sticky Bit”
- Only used while doing calculations
- Not stored in the float itself
- The mantissa is shifted in calculations to align radix
- The guard bits and round bits are extra precision
- The sticky bit is an OR of anything that shifts through it
Special bits
- “Guard Bit”, “Round Bit”, “Sticky Bit”
- [G][R][S]
- [0][-][-] - Round Down (do nothing)
- [1][0][0] - Round Up if the mantissa LSB is 1
- [1][0][1] - Round Up
- [1][1][0] - Round Up
- [1][1][1] - Round Up
Significance Error
- Compute the Area of a Triangle given side lengths
- Hero(n)’s Formula:
- Take \(s = \frac{1}{2}(a + b + c)\)
- Then \(\sqrt{s(s-a)(s-b)(s-c)}\)
- Kahan’s Algorithm:
- Take \(((a, b, c) | a \leq b \leq c)\)
- Then \(\sqrt{\frac{(x + (y + z)) \times (z - (x - y)) \times (z + (x - y)) \times (x + (y - z))}{4}}\)
Write them
src/lib.rs
fn heron(a:f32, b:f32, c:f32) -> f32 {
let s = (a + b + c)/2.0_f32;
return (s * (s - a) * (s - b) * (s - c)).sqrt();
}
fn kahan(a:f32, b:f32, c:f32) -> f32 {
let mut s = vec![a,b,c];
s.sort_by(|a, b| a.partial_cmp(b).unwrap()); // "partial"? Why not `.sort`?
let mut prod = s[0] + s[1] + s[2];
prod *= s[2] - (s[0] - s[1]);
prod *= s[2] + (s[0] - s[1]);
prod *= s[0] + (s[1] - s[2]);
return prod.sqrt() / 4.0;
}Test them
src/main.rs
- Oh what’s that?
[src/main.rs:21:5] heron(3.0,4.0,5.0) = 6.0
[src/main.rs:22:5] kahan(3.0,4.0,5.0) = 6.0
[src/main.rs:25:5] heron(a,a,c) = 781.25006
[src/main.rs:26:5] kahan(a,a,c) = 500.0- Using
f64(vsf32) we get 499.9999999999994
Significance Error
- Use Stable Algorithms
- Keep big numbers with big numbers, little numbers with little numbers.
- Parentheses can help
- The compiler won’t re-arrange your math if it cannot prove it would yield the same!
- E.g. you can’t use
<in Rust as you may provide aNaN.
- E.g. you can’t use
Significance Error – Don’t floats?
- Use integers
- Very fast
- Trade more precision for less range
- Only input/output may be impacted by floating point conversions
- Financial applications represent dollars as only cents or tenth’s of cents
Significance Error – Don’t floats?
- Use a math library
- Slower
- Define your own level of accuracy
- Usually GMP or hardware specific.
Significance Error – Don’t floats?
- Execute symbolically
- Slowest
- Arbitrary accuracy
- Round only at output
Significance Error – Don’t floats?
- Write your own library?
- Use vectors of bits or bytes.
- Write your own arithmetic operations.
- Test and debug your own implemention.
- Coming soon to a homework near you!
Algebraic Assumption Error
- Distributive Rule does not apply:
- \(a = x \times y - x \times z \nRightarrow a = x (y - z)\)
- Associative Rule does not apply: 𝑥 + 𝑦 +𝑧 ≠ 𝑥 +𝑦 +𝑧
- \(a = x + (y + z) \nRightarrow a = (x + y) + z\)
- Cannot interchange division and multiplication:
- \(a = \frac{x}{10.0} \nRightarrow a = x \times 0.1\)
Distribution
Association
Interchange
- Check last digit
Floating Point Exceptions
| IEEE 754 Exception | Result when traps disabled | Argument to trap handler |
|---|---|---|
| overflow | \(\pm \infty\) or \(\pm x_{\text{max}}\) | \(\text{round}(x 2^{-a})\) |
| underflow | \(0, \pm 2^{\text{min}}\) or denormalized | \(\text{round}(x 2^{a})\) |
| divide by zero | \(\pm \infty\) | invalid operation |
| invalid | \(\text{NaN}\) | invalid operation |
| inexact | \(\text{round}(x)\) | \(\text{round}(x)\) |
But Wait! There’s More!
- Binary to Decimal Conversion Error
- Summation Error
- Propagation Error
- Underflow, Overflow
- Type Narrowing/Widening Rules
Testing
- Design for Numerical Stability
- Perform Meaningful Testing
- Document assumptions
- Track sources of approximation
- Quantify goodness
- Well conditioned algorithms
- Backward error analysis
- Are the outputs identical for slightly modified inputs?
Today
- Understand precision through the lens of floats.
- Understand the basics of floats
- Understand the language of floats
- Get a feel for when further investigation is required