IEEE 754

Systems in Rust

Prof. Calvin

Announcements

  • Welcome to Systems in Rust
  • Action Items:
    • “SHA-512” is due on next Friday
    • Lecture on numbers, inspired by the lab, while we wait.

Today

  • Understand precision through the lens of floats.
    • Understand the basics of floats
    • Understand the language of floats
    • Get a feel for when further investigation is required

Citation

  • Yoinked
  • url
  • Author John Farrier, Booz Allen Hamilton

Mission Statement

  • I’m a normal person.
    • I think 5/2 is 2.5 or perhaps 2½.
  • I’m a scientist.
    • I’m solving “Black-Scholes”
    • Does anyone know what this is doing? \[ d_2 = d_1 - \sigma\sqrt{T - t} = \frac{1}{\sigma\sqrt{T - t}}\left[\ln\left(\frac{S_t}{K}\right) + \left(r - q - \frac{1}{2}\sigma^2\right)(T - t)\right] \]

Common Fallacies

  • “Floating point numbers are numbers”
    • max(count()) Pinocchios
  • “It’s floating point error”
    • “All floating point involves magical rounding errors”
  • “Linux and Windows handle floats differently”
  • “Floating point represents an interval value near the actual value”

Common Fallacies 2.0

  • “A double (an f64) holds 15 decimal places and I only need 3, so I have nothing to worry about”1
  • “My programming language does better math than your programming language”2
  • “Why can’t computers just store whatever number I use”3

Anatomy of IEEE Floats

IEEE Float Specification

  • IEEE 754-1985, IEEE 854-1987, IEEE 754-2008
    • These are paywalled.
    • Those are years.
  • Provide for portable, provably consistent math
    • Consistent, not correct.

Assurances

  • Ensure some significant mathematical identities hold true:
    • \(x + y = y + x\)
      • Symmetry of addition
    • \(x + 0 = x\)
      • Additive identity
    • \(x = y \implies x - y = 0\)
      • Identity under subtraction

Assurances 2.0

\[ \frac{x}{\sqrt{x^2+y^2}} \leq 1 \]

  • What is missing?

IEEE Float Specification

  • Ensure every floating point number is unique
  • Ensure every floating point number has an opposite
    • Zero is a special case because of this
  • Specifies algorithms for addition, subtraction, multiplication, division, and square-root
    • Not really operations/relations! They are algorithms.

Aside: Scientific Notation

Scientific notation is a way of expressing numbers that are too large or too small to be conveniently written in decimal form, since to do so would require writing out an inconveniently long string of digits.

  • In scientific notation, nonzero numbers are written in the form

\[a \times 10^b\]

Aside: Explanation

  • In scientific notation, nonzero numbers are written in the form

\[a \times 10^b\]

  • \(a\) (the coefficient or mantissa) is a number greater than or equal to 1 and less than 10 (\(1 \le |a| < 10\)).
  • \(10\) is the base.
  • \(b\) (the exponent) is an integer.

Aside: Physical Examples

  1. Speed of light: The speed of light in a vacuum is approximately \(300,000,000 \text{ m/s}\) \[ 3 \times 10^8 \text{ m/s} \]

  2. Mass of an electron: The mass of an electron is approximately \(0.00000000000000000000000000091093837 \text{ g}\). \[ 9.1093837 \times 10^{-28} \text{ g} \]

Aside: Economic Examples

IEEE Layout

  • An approximation using scientific notation
    • \(x = -1^s \times 2^e \times 1.m\)
    • \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1.\text{mantissa}\)
      • Where the mantissa is the technical term for the the digits after the decimal point.

With Binary

  • \(x = -0b1^{\text{0b0}} \times 0b10^{\text{0b10000000}} \times 0b1.10010010000111111011011\)
  • Express in memory as the concatenation:
    • 0b0 to 0b10000000 to 0b10010010000111111011011
    • 01000000010010010000111111011011

Singles and Doubles

  • 32 - bits = 1 sign bit + 8 exponent bits + 23 mantissa bits
    • 0b0 to 0b10000000 to 0b10010010000111111011011
  • 64 - bits = 1 sign bit + 12 exponent bits + 52 mantissa bits

Understanding check

  • What is the probability a real number \(a \in \mathbb{R}\) has an exact float representation?
  • What is the probability an integer \(n \in \mathbb{Z}\) has an exact float representation?
  • What is the probability a course number \(n < 600\) has an exact float representation?

Special Floats - NaN

  • Divide by Zero
    • 1 / 0
  • Not a Number (NaN)
>>> from numpy import float32 as f32
>>> f32(1)/f32(0)
<stdin>:1: RuntimeWarning: divide by zero encountered in scalar divide
np.float32(inf)
>>> 1/0
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero

Special Floats - inf

  • Signed Infinity
    • Overflow protection
    >>> f32(10) ** f32(100)
<stdin>:1: RuntimeWarning: overflow encountered in scalar power
np.float32(inf)
>>> 10.0 ** 10000
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
OverflowError: (34, 'Numerical result out of range')

Infinity is signed

  • We can get negative infinity through a variety of means.
>>> -(f32(10) ** f32(100))
np.float32(-inf)
  • We note that this suppresses the overflow error use ()
  • In some languages this is not ever regarded as an overflow error, like Julia (where we have to use larger powers due to the f64 default)
julia> 10.0^10000
Inf

julia> -(10.0^10000)
-Inf

Signed Zero

  • Signed Zero
    • Underflow protection, preserves sign
      • 0 =− 0
    >>> -1 / 10 ** 1000
-0.0
>>> 0.0 == (-1 / 10 ** 1000)
True
>>> -0.0
-0.0
>>> 0.0 - 0.0
0.0
  • Works in base Python (e.g. don’t need NumPy).
  • Couldn’t get it to work in Julia actually (went to -inf or NaN)

Simple Example

  • Floating point is great because it will work exactly how you expect.
>>> 0.1 + 0.2 == 0.3
False
  • More or less.
>>> 0.1 + 0.2
0.30000000000000004

Simple Example

  • We shouldn’t be suprised by this!
>>> _ = [print(f"{f32(i/10):1.100}") for i in range(1,4)]
0.100000001490116119384765625
0.20000000298023223876953125
0.300000011920928955078125
>>> _ = [print(f"{f64(i/10):1.100}") for i in range(1,4)]
0.1000000000000000055511151231257827021181583404541015625
0.200000000000000011102230246251565404236316680908203125
0.299999999999999988897769753748434595763683319091796875

Storage of 1.

  • \(x = -1^s \times 2^e \times 1.m\)
  • \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1.\text{mantissa}\)
  • \(x = -1^{\text{sign bit}} \times \text{base} 2^{\text{exponent}} \times 1 + \text{mantissa} \times \frac{1}{2^n}\)
  • \(1 = -1^0 \times 2^0 \times (1 + 0 \times \frac{1}{2^n}\)
  • So each of the sign bit, the base, and the mantissa are zero.
    • I should note I was unable to reproduce this in Rust or C.
    • I’m not really a floating pointer.

Except…

  • This is actually a little bit fake.
$ cat src/main.rs
fn main() {
    let x:f32 = 1.0;
    println!("{:032b}", x.to_bits());
}
$ cargo run
    Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.00s
     Running `target/debug/bits`
00111111100000000000000000000000
  • What is that?

Shift 127

While the exponent can be positive or negative, in binary formats it is stored as an unsigned number that has a fixed “bias” added to it.

  • The IEEE 754 binary format specifies a hardware implementation of such that the exponent, be it positive or negative, in binary formats is stored as an unsigned number that has a fixed “bias” added to it.
  • In the case of 32 bit floats, the bias is 127.

Breakdown

  • Take the following:
00111111100000000000000000000000
  • That is:
    • Sign bit of 0
    • Exponent of 01111111
      • All zeroes and all ones are reserved for NaN, inf, etc.
    • Mantissa of 23 zeroes.

How precise?

  • I have referred to f32 as having “32 bits of precision”.
  • How much precision is that?
  • Well, let’s set the least significant bit of the mantissa to one.
main.rs
fn main() {
    let x:f32 = 1.0;
    let mut b:u32 = x.to_bits();
    b |= 1;
    println!("{:032b}", b);
    println!("{:1.32}", f32::from_bits(b));
}

“Epsilon”

  • What do we get?
$ cargo run
    Finished `dev` profile [unoptimized + debuginfo] target(s) in 0.00s
     Running `target/debug/bits`
00111111100000000000000000000001
1.00000011920928955078125000000000
  • We refer to this value (less one) as machine epsilon, or perhaps \(\varepsilon\).
  • The difference between 1.0 and the next available floating point number.
  • Much lower, of course, with double and quad precision.

Easier: “Sig figs”

Format Sign Exp. Mant. Bits Bias Prec. Significance
Half 1 5 10 16 15 11 3-4
Single 1 8 23 32 127 24 6-9
Double 1 11 52 64 1023 53 15-17
Quad 1 15 112 128 16383 113 33-36

Sig figs

  • IEEE 754 was intended for scientific computing
  • That is, not systems computing, software etc.
  • Useful to us to think about information and how bits work.

Significant figures, also referred to as significant digits, are specific digits within a number that is written in positional notation that carry both reliability and necessity in conveying a particular quantity.

Small Values

  • For 32-bit floats, the minimum base 10 exponent is -36.
  • How is \(1.0 \times 10^{-37}\) represented?
// In Rust, we may use '0b' prefix for binary representation.
// In Rust, we may us underscores within numerical values.
0b0_00000000_11011001110001111101110

Test it

  • Write a simple test…
src/main.rs
fn main() {
    let b:u32 = 0b0_00000000_11011001110001111101110;
    println!("{:032b}", b);
    println!("{:1.100}", f32::from_bits(b));
    let x:f32 = 10.0_f32.powf(-38.0_f32);
    println!("{:032b}", x.to_bits());
    println!("{:1.100}", x);
}
  • Results are as expected.
00000000011011001110001111101110
0.0000000000000000000000000000000000000099999993504564039245746141539976645128551939195729831580121175
00000000011011001110001111101110
0.0000000000000000000000000000000000000099999993504564039245746141539976645128551939195729831580121175

“Denormalized Number”

  • Numbers that have a zero exponent
  • Required when the exponent is below the minimum exponent
  • Helps prevent underflow
  • Generally speaking, if you are using one these, the math is about to get wronger than you’d think.
  • The good (???) language C++ provides a std::nextafter for which Rust crates exist.

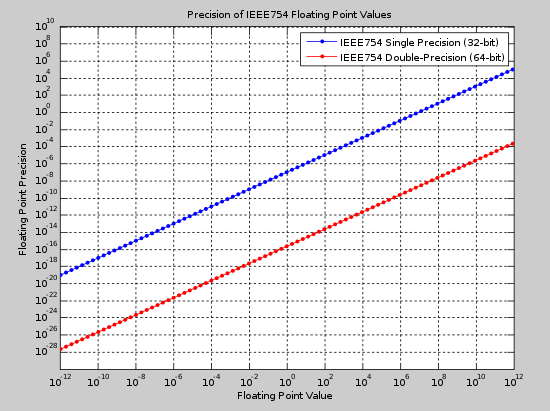
Floating Point Precision

  • Representation is not uniform between numbers
  • Most precision lies between 0.0 and 0.1
  • Precision falls away

Visually

Floating Point Precision

The number of floats from 0.0

  • … to 0.1 = 1,036,831,949
  • … to 0.2 = 8,388,608
  • … to 0.4 = 8,388,608
  • … to 0.8 = 8,388,608
  • … to 1.6 = 8,388,608
  • … to 3.2 = 8,388,608

Errors in Floating Point

  • Storage of \(\pi\)
>>> from numpy import pi as pi
>>> # copy paste Wolfram|Alpha
>>> '3.14159265358979323846264338327950288419716939937510582097494459230781640628'
'3.14159265358979323846264338327950288419716939937510582097494459230781640628'
>>> f'{pi:1.100}'
'3.141592653589793115997963468544185161590576171875'
  • They differ fairly early on!

Measuring Error: “Ulps”

  • Units in Last Place

In computer science and numerical analysis, unit in the last place or unit of least precision (ulp) is the spacing between two consecutive floating-point numbers, i.e., the value the least significant digit (rightmost digit) represents if it is 1. It is used as a measure of accuracy in numeric calculations.

Haskell

  • Usually ULP is taught using Haskell.
> until (\x -> x == x+1) (+1) 0 :: Float
1.6777216e7
> it-1
1.6777215e7
> it+1
1.6777216e7
  • I’ll translate to .py/.rs

Generators

  • By convention we check number theoretic results with lazily evaluated generator expressions in Python.
  • The following generators all powers of two for a which adding one does not change the value within Python floating points.
from itertools import count

gen = (i for i in count() if 2.0 ** float(i) + 1.0 == 2.0 ** float(i))

x = next(gen)

print('2.0 ** x + 0.0 = ', 2.0 ** x + 0.0)
print('2.0 ** x + 1.0 = ', 2.0 ** x + 1.0)

Iterators

  • Rust doesn’t require iterators, supporting the infinite iterator by default using unwrap.
let x = (0..).find(|&i| f64::powi(2.0, i) + 1.0 == f64::powi(2.0, i)).unwrap();

let base = f64::powi(2.0, x);

// Prints the result (2^53 = 9007199254740992.0)
println!("2.0 ** x + 0.0 = {:.1}", base);
println!("2.0 ** x + 1.0 = {:.1}", base + 1.0);
  • I haven’t used find before, this is an LLM donation to our knowledge base.
  • By the way, that is basically 2 ** 53 and there are 52 bits of mantissa precision.

On “Ulps”

  • We can measure error using ULPs.

The gap between the two floating-point numbers nearest to x, even if x is one of )them.

>>> from numpy import float32 as f32, pi as pi, float64 as f64
>>> f64(pi) - f64(f32(pi))
np.float64(-8.742278012618954e-08)

Rounding

  • We have some guarantees:
    • IEEE 754 requires that that elementary arithmetic operations are correctly rounded to within 0.5 ulps
    • Transcendental functions are generally rounded to between 0.5 and 1.0 ulps
      • Transcendental as in \(\pi\) or \(e\)
  • ~9 ulps

Relative Error

  • The difference between the “real” number and the approximated number, divided by the “real” number.
>>> f64(f32(pi))/f64(pi)
np.float64(1.0000000278275352)
  • So for pi in f32, around \(2.9 \times 10^{-8}\)

Rounding Error

  • Induced by approximating an infinite range of numbers into a finite number of bits
  • Rounding is:
    • Towards the nearest
    • Towards zero
    • Towards positive infinity (round up)
    • Towards negative infinity (round down)

Rounding Error

  • What about rounding the half-way case? (i.e. 0.5)
    • Round Up vs. Round Even
  • Correct Rounding:
    • Basic operations (add, subtract, multiply, divide, sqrt) should return the number nearest the mathematical result.
    • If there is a tie, round to the number with an even mantissa

Implementation

  • “Guard Bit”, “Round Bit”, “Sticky Bit”
  • Only used while doing calculations
    • Not stored in the float itself
    • The mantissa is shifted in calculations to align radix
  • The guard bits and round bits are extra precision
  • The sticky bit is an OR of anything that shifts through it
0_00000000_00000000000000000000000_G_R_S..

Special bits

  • “Guard Bit”, “Round Bit”, “Sticky Bit”
  • [G][R][S]
  • [0][-][-] - Round Down (do nothing)
  • [1][0][0] - Round Up if the mantissa LSB is 1
  • [1][0][1] - Round Up
  • [1][1][0] - Round Up
  • [1][1][1] - Round Up
0_00000000_00000000000000000000000_G_R_S..

Significance Error

  • Compute the Area of a Triangle given side lengths
  • Hero(n)’s Formula:
    • Take \(s = \frac{1}{2}(a + b + c)\)
    • Then \(\sqrt{s(s-a)(s-b)(s-c)}\)
  • Kahan’s Algorithm:
    • Take \(((a, b, c) | a \leq b \leq c)\)
    • Then \(\sqrt{\frac{(x + (y + z)) \times (z - (x - y)) \times (z + (x - y)) \times (x + (y - z))}{4}}\)

Write them

src/lib.rs
fn heron(a:f32, b:f32, c:f32) -> f32 {
    let s = (a + b + c)/2.0_f32;
    return (s * (s - a) * (s - b) * (s - c)).sqrt();
}

fn kahan(a:f32, b:f32, c:f32) -> f32 {
    let mut s = vec![a,b,c];
    s.sort_by(|a, b| a.partial_cmp(b).unwrap()); // "partial"? Why not `.sort`?
    let mut prod = s[0] + s[1] + s[2];
    prod *= s[2] - (s[0] - s[1]);
    prod *= s[2] + (s[0] - s[1]);
    prod *= s[0] + (s[1] - s[2]);
    return prod.sqrt() / 4.0;
}

Test them

src/main.rs
fn main(){
    dbg!(heron(3.0,4.0,5.0));
    dbg!(kahan(3.0,4.0,5.0));
    let a = 100_000.0_f32;
    let c = 0.01_f32;
    dbg!(heron(a,a,c));
    dbg!(kahan(a,a,c));
}
  • Oh what’s that?
[src/main.rs:21:5] heron(3.0,4.0,5.0) = 6.0
[src/main.rs:22:5] kahan(3.0,4.0,5.0) = 6.0
[src/main.rs:25:5] heron(a,a,c) = 781.25006
[src/main.rs:26:5] kahan(a,a,c) = 500.0
  • Using f64 (vs f32) we get 499.9999999999994

Significance Error

  • Use Stable Algorithms
    • Keep big numbers with big numbers, little numbers with little numbers.
  • Parentheses can help
  • The compiler won’t re-arrange your math if it cannot prove it would yield the same!
    • E.g. you can’t use < in Rust as you may provide a NaN.

Significance Error – Don’t floats?

  • Use integers
    • Very fast
    • Trade more precision for less range
    • Only input/output may be impacted by floating point conversions
    • Financial applications represent dollars as only cents or tenth’s of cents

Significance Error – Don’t floats?

  • Use a math library
    • Slower
    • Define your own level of accuracy
    • Usually GMP or hardware specific.

Significance Error – Don’t floats?

  • Execute symbolically
    • Slowest
    • Arbitrary accuracy
    • Round only at output

Significance Error – Don’t floats?

  • Write your own library?
    • Use vectors of bits or bytes.
    • Write your own arithmetic operations.
    • Test and debug your own implemention.
  • Coming soon to a homework near you!

Algebraic Assumption Error

  • Distributive Rule does not apply:
    • \(a = x \times y - x \times z \nRightarrow a = x (y - z)\)
  • Associative Rule does not apply: 𝑥 + 𝑦 +𝑧 ≠ 𝑥 +𝑦 +𝑧
    • \(a = x + (y + z) \nRightarrow a = (x + y) + z\)
  • Cannot interchange division and multiplication:
    • \(a = \frac{x}{10.0} \nRightarrow a = x \times 0.1\)

Distribution

>>> x, y, z
(np.float32(1000000000.0), np.float32(1.0000005), np.float32(1.0))
>>> x * y - x * z ; x * (y - z)
np.float32(448.0)
np.float32(476.83716)

Association

>>> x, y, z
(np.float32(16777216.0), np.float32(1.0), np.float32(1.0))
>>> x + (y + z) ; (x + y) + z
np.float32(16777218.0)
np.float32(16777216.0)

Interchange

  • Check last digit
>>> 1 / 7 / 100000000
1.4285714285714284e-09
>>> 1 / 100000000 / 7
1.4285714285714286e-09

Floating Point Exceptions

IEEE 754 Exception Result when traps disabled Argument to trap handler
overflow \(\pm \infty\) or \(\pm x_{\text{max}}\) \(\text{round}(x 2^{-a})\)
underflow \(0, \pm 2^{\text{min}}\) or denormalized \(\text{round}(x 2^{a})\)
divide by zero \(\pm \infty\) invalid operation
invalid \(\text{NaN}\) invalid operation
inexact \(\text{round}(x)\) \(\text{round}(x)\)

But Wait! There’s More!

  • Binary to Decimal Conversion Error
  • Summation Error
  • Propagation Error
  • Underflow, Overflow
  • Type Narrowing/Widening Rules

Testing

  • Design for Numerical Stability
  • Perform Meaningful Testing
  • Document assumptions
  • Track sources of approximation
  • Quantify goodness
    • Well conditioned algorithms
  • Backward error analysis
    • Are the outputs identical for slightly modified inputs?

Today

  • Understand precision through the lens of floats.
    • Understand the basics of floats
    • Understand the language of floats
    • Get a feel for when further investigation is required